This code is uses machine learning in Python to optimize the design of an energy system. The energy system is defined by two variables: the energy input (in MW) and the efficiency of the system (dimensionless). The goal is to predict the cost of the energy system as a function of these variables.
To do this, the code first defines a function called cost that calculates the cost of the energy system as a function of the energy input and the efficiency. This function takes into account the cost of the energy input itself, as well as the efficiency of the system (since a more efficient system will have a lower cost).
Next, the code generates a training dataset by randomly sampling a large number of values for the energy input and efficiency. The machine learning model (a random forest regressor) is then trained on this dataset using the fit function.
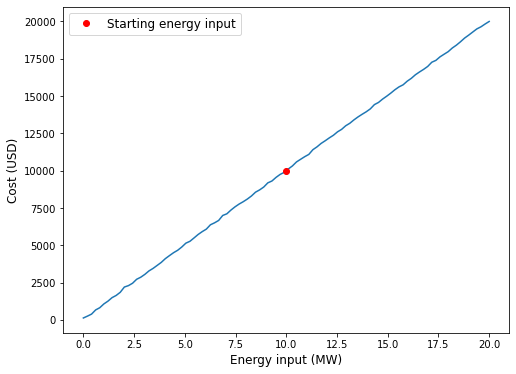
The code then generates a prediction dataset and uses the machine learning model to predict the cost for this dataset using the predict function. The resulting predictions are plotted as a function of the energy input, with the starting energy input indicated by a red dot. The resulting plot can be used to visualize how the predicted cost of the energy system changes as a function of the energy input and efficiency.
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed Dec 21 23:01:06 2022
@author: ramnot
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
# Define variables for the energy system
energy_input = 10 # MW
energy_output = 8 # MW
efficiency = energy_output / energy_input # dimensionless
# Define the cost function
def cost(energy_input, efficiency):
# Assume a cost of $1000/MW for energy input
return energy_input * 1000 + efficiency**2
# Generate a training dataset
num_samples = 1000
X_train = np.random.uniform(0, 20, (num_samples, 2))
y_train = cost(X_train[:,0], X_train[:,1])
# Use machine learning to predict the cost as a function of the energy input and efficiency
model = RandomForestRegressor()
model.fit(X_train, y_train)
# Generate a prediction dataset
energy_input_range = np.linspace(0, 20, 100)
X_pred = np.column_stack((energy_input_range, np.ones_like(energy_input_range)*efficiency))
# Use the machine learning model to predict the cost for the prediction dataset
y_pred = model.predict(X_pred)
# Plot the predicted cost as a function of the energy input
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(energy_input_range, y_pred)
ax.plot(energy_input, cost(energy_input, efficiency), 'o', color='red', label='Starting energy input')
ax.set_xlabel('Energy input (MW)', fontsize=12)
ax.set_ylabel('Cost (USD)', fontsize=12)
ax.legend(fontsize=12)
plt.show()