Optimize a manufacturing process

This code is an example of how to use Python to optimize a manufacturing process. The manufacturing process is defined by two parameters: the strength of the material and the density of the material. The goal is to find the optimal values of these parameters that will result in a final product with a strength and density that are as close as possible to the desired values.

To do this, the code defines a function called manufacturing_cost that calculates the difference between the desired product properties and the actual product properties. This function is used as an objective function that we want to minimize.

Then, the code defines a function called optimize_manufacturing_process that uses an optimization algorithm to find the optimal values of the manufacturing parameters. The optimization algorithm is given the starting values of the manufacturing parameters (the strength and density of the starting material), and it iteratively adjusts these values to find the minimum of the manufacturing_cost function.

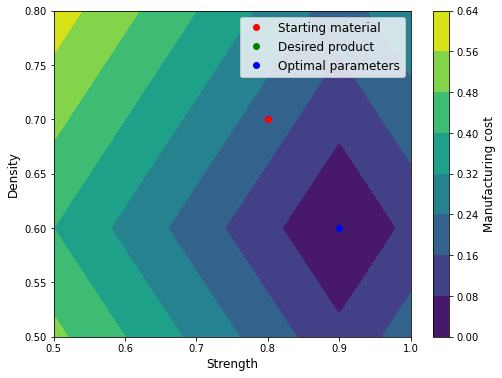
Finally, the code generates a grid of possible manufacturing parameter values and calculates the manufacturing cost at each point on the grid. It then plots the manufacturing cost as a function of the manufacturing parameters, with the optimal parameters indicated by a blue dot. The resulting plot can be used to visualize how the manufacturing cost changes as a function of the manufacturing parameters, and to see how close the optimal parameters are to the desired product properties.

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed Dec 21 22:33:26 2022

@author: ramnot
"""

import numpy as np
import scipy.optimize as optimize
import matplotlib.pyplot as plt

# Define variables for the manufacturing process
material_properties = {'strength': 0.8, 'density': 0.7}
desired_product_properties = {'strength': 0.9, 'density': 0.6}

# Define the manufacturing cost function
def manufacturing_cost(parameters, desired_product_properties):
  strength_cost = abs(parameters[0] - desired_product_properties['strength'])
  density_cost = abs(parameters[1] - desired_product_properties['density'])
  return strength_cost + density_cost

# Use optimization algorithm to find the optimal manufacturing parameters
def optimize_manufacturing_process(material_properties, desired_product_properties):
  result = optimize.minimize(manufacturing_cost, [material_properties['strength'], material_properties['density']], args=(desired_product_properties,), method='nelder-mead')
  return result.x

optimal_parameters = optimize_manufacturing_process(material_properties, desired_product_properties)

# Generate a grid of manufacturing parameter values
strength_range = np.linspace(0.5, 1, 100)
density_range = np.linspace(0.5, 0.8, 100)
strength_values, density_values = np.meshgrid(strength_range, density_range)

# Calculate the manufacturing cost at each point on the grid
cost_values = np.zeros_like(strength_values)
for i in range(strength_values.shape[0]):
  for j in range(strength_values.shape[1]):
    cost_values[i,j] = manufacturing_cost([strength_values[i,j], density_values[i,j]], desired_product_properties)

# Plot the manufacturing cost as a function of the manufacturing parameters
fig, ax = plt.subplots(figsize=(8,6))
contour = ax.contourf(strength_values, density_values, cost_values, cmap='viridis')
cbar = fig.colorbar(contour)
cbar.ax.set_ylabel('Manufacturing cost', rotation=90, fontsize=12)
ax.plot(material_properties['strength'], material_properties['density'], 'o', color='red', label='Starting material')
ax.plot(desired_product_properties['strength'], desired_product_properties['density'], 'o', color='green', label='Desired product')
ax.plot(optimal_parameters[0], optimal_parameters[1], 'o', color='blue', label='Optimal parameters')
ax.set_xlabel('Strength', fontsize=12)
ax.set_ylabel('Density', fontsize=12)
ax.legend(fontsize=12)
plt.show()

Latest News